2024 लेखक: Howard Calhoun | [email protected]. अंतिम बार संशोधित: 2023-12-17 10:28
विचरण बहुभिन्नरूपी विश्लेषण विभिन्न सांख्यिकीय विधियों का एक संयोजन है जो परिकल्पनाओं और अध्ययन के तहत कारकों और कुछ विशेषताओं के बीच संबंध का परीक्षण करने के लिए डिज़ाइन किया गया है जिनका मात्रात्मक विवरण नहीं है। साथ ही, यह तकनीक आपको कुछ प्रक्रियाओं पर कारकों की बातचीत और उनके प्रभाव की डिग्री निर्धारित करने की अनुमति देती है। ये सभी परिभाषाएं काफी भ्रमित करने वाली लगती हैं, तो आइए अपने लेख में इन्हें और विस्तार से समझते हैं।
मानदंड और विचरण के विश्लेषण के प्रकार
विचरण बहुभिन्नरूपी विश्लेषण की विधि का उपयोग अक्सर निरंतर मात्रात्मक चर और नाममात्र गुणात्मक लक्षणों के बीच संबंध खोजने के लिए किया जाता है। वास्तव में, यह तकनीक विभिन्न अंकगणितीय नमूनों की समानता के बारे में विभिन्न परिकल्पनाओं का परीक्षण है। इस प्रकार, यह कर सकते हैंमाना जाता है और कई नमूनों की तुलना करने के लिए एक मानदंड के रूप में माना जाता है। हालाँकि, परिणाम समान होंगे यदि तुलना के लिए केवल दो तत्वों का उपयोग किया जाता है। टी-टेस्ट के अध्ययन से पता चलता है कि यह तकनीक आपको किसी अन्य ज्ञात विधि की तुलना में परिकल्पना की समस्या का अधिक विस्तार से अध्ययन करने की अनुमति देती है।
इस तथ्य पर ध्यान नहीं देना भी असंभव है कि विचरण के कुछ प्रकार के विश्लेषण एक निश्चित कानून पर आधारित होते हैं: अंतरसमूह विचलन के वर्गों का योग और इंट्राग्रुप विचलन के वर्गों का योग बिल्कुल बराबर होता है। एक अध्ययन के रूप में, फिशर टेस्ट का उपयोग किया जाता है, जिसका उपयोग इंट्रा-ग्रुप वेरिएंस के विस्तृत विश्लेषण के लिए किया जाता है। यद्यपि इसके लिए वितरण की सामान्यता के साथ-साथ नमूनों की समरूपता - भिन्नताओं की समानता के लिए किसी और चीज की आवश्यकता होती है। विचरण के विश्लेषण के प्रकार के लिए, निम्नलिखित प्रतिष्ठित हैं:
- बहुभिन्नरूपी या बहुभिन्नरूपी विश्लेषण;
- एकतरफा या एकतरफा विश्लेषण।
यह अनुमान लगाना मुश्किल नहीं है कि दूसरा एक विशेषता की निर्भरता और अध्ययन के तहत मूल्य पर विचार करता है, और पहला एक साथ कई विशेषताओं के विश्लेषण पर आधारित है। इसके अलावा, बहुभिन्नरूपी विचरण आपको कई तत्वों के बीच एक मजबूत संबंध की पहचान करने की अनुमति नहीं देता है, क्योंकि एक ही बार में कई मूल्यों की निर्भरता की जांच की जाती है (हालांकि विधि का संचालन करना बहुत आसान है)।
कारक
बहुभिन्नरूपी सहसंबंध विश्लेषण के तरीकों के बारे में सोचा? तब आपको पता होना चाहिए कि विस्तृत अध्ययन के लिए आपको उन कारकों का अध्ययन करना चाहिए जो प्रयोग की परिस्थितियों को नियंत्रित करते हैं और अंतिम परिणाम को प्रभावित करते हैं। इसके तहतकारक प्रसंस्करण मूल्यों के तरीकों और स्तरों को इंगित कर सकते हैं जो किसी विशेष स्थिति की एक विशेष अभिव्यक्ति की विशेषता रखते हैं। इस मामले में, आंकड़े क्रमिक या नाममात्र माप प्रणाली में दिए गए हैं। यदि डेटा ग्रुपिंग में कोई समस्या है, तो आपको उन्हीं संख्यात्मक मानों का उपयोग करना होगा, जो अंतिम परिणाम को थोड़ा बदल देते हैं।

यह भी समझना चाहिए कि अवलोकनों और समूहों की संख्या अत्यधिक बड़ी नहीं हो सकती है, क्योंकि इससे डेटा की अधिकता होती है और गणना को पूरा करने में असमर्थता होती है। इसी समय, समूहीकरण की विधि न केवल मात्रा पर निर्भर करती है, बल्कि कुछ मूल्यों की भिन्नता की प्रकृति पर भी निर्भर करती है। विश्लेषण में अंतराल के आकार और संख्या को समान आवृत्तियों के सिद्धांत के साथ-साथ उनके बीच समान अंतराल द्वारा निर्धारित किया जा सकता है। नतीजतन, सभी प्राप्त अध्ययनों को बहुभिन्नरूपी विश्लेषण के आंकड़ों में सूचीबद्ध किया जाएगा, जो विभिन्न उदाहरणों पर आधारित होना चाहिए। हम इस पर बाद के खंडों में लौटेंगे।
एनोवा का उद्देश्य
इसलिए, कभी-कभी ऐसी स्थितियां उत्पन्न हो सकती हैं जब दो या दो से अधिक विभिन्न नमूनों की तुलना करना आवश्यक हो। इस मामले में, प्रतिगमन की डिग्री में परिकल्पना के अध्ययन और विभिन्न कारकों के संबंध के आधार पर एक बहुभिन्नरूपी सहसंबंध-प्रतिगमन विश्लेषण लागू करना सबसे तार्किक होगा। साथ ही, तकनीक का नाम इस तथ्य को इंगित करता है कि शोध प्रक्रिया में विचरण के विभिन्न घटकों का उपयोग किया जाता है।

अध्ययन का सार क्या है? के लियेसबसे पहले, दो या दो से अधिक संकेतक अलग-अलग हिस्सों में विभाजित होते हैं, जिनमें से प्रत्येक एक निश्चित कारक की कार्रवाई से मेल खाता है। उसके बाद, विभिन्न नमूनों के संबंध और उनके बीच संबंधों की खोज के लिए कई शोध प्रक्रियाएं की जाती हैं। ऐसी जटिल लेकिन दिलचस्प तकनीक को और अधिक विस्तार से समझने के लिए, हम अनुशंसा करते हैं कि आप हमारे लेख के निम्नलिखित अनुभागों में दिए गए बहुभिन्नरूपी सहसंबंध विश्लेषण के कई उदाहरणों का अध्ययन करें।
उदाहरण एक
उत्पादन कार्यशाला में कई स्वचालित मशीनें हैं, जिनमें से प्रत्येक को एक विशिष्ट भाग का उत्पादन करने के लिए डिज़ाइन किया गया है। उत्पादित तत्व का आकार एक यादृच्छिक चर है, जो न केवल मशीन की सेटिंग्स पर निर्भर करता है, बल्कि यादृच्छिक विचलन पर भी निर्भर करता है जो अनिवार्य रूप से भागों के उत्पादन के परिणामस्वरूप होगा। लेकिन एक कार्यकर्ता मशीन के सही संचालन का निर्धारण कैसे कर सकता है यदि वह शुरू में दोषों के साथ भागों का उत्पादन करता है? यह सही है, आपको बाजार पर उसी हिस्से को खरीदने और उत्पादन के दौरान प्राप्त होने वाले आयामों की तुलना करने की आवश्यकता है। उसके बाद, आप उपकरण को समायोजित कर सकते हैं ताकि यह वांछित आकार के भागों का उत्पादन करे। और इससे कोई फर्क नहीं पड़ता कि कोई निर्माण दोष है, क्योंकि गणनाओं में इसे भी ध्यान में रखा जाता है।

उसी समय, यदि मशीनों पर कुछ संकेतक हैं जो आपको समायोजन की तीव्रता (एक्स और वाई अक्ष, गहराई, और इसी तरह) निर्धारित करने की अनुमति देते हैं, तो सभी मशीनों पर संकेतक पूरी तरह से अलग होंगे. यदि माप बिल्कुल समान निकला, तो निर्माण दोष नहीं हो सकताबिल्कुल ध्यान में रखना। हालांकि, ऐसा बहुत कम ही होता है, खासकर अगर त्रुटियों को मिलीमीटर में मापा जाता है। लेकिन अगर जारी किए गए हिस्से में बाजार पर खरीदे गए मानक के समान आयाम हैं, तो किसी भी शादी का कोई सवाल ही नहीं हो सकता है, क्योंकि "आदर्श" के उत्पादन में एक मशीन का भी इस्तेमाल किया गया था, जिसमें कुछ त्रुटियां थीं, जो शायद भी थीं श्रमिकों द्वारा ध्यान में रखा गया।
दूसरा उदाहरण
विद्युत पर चलने वाले एक निश्चित उपकरण के निर्माण के लिए, कई प्रकार के विभिन्न इन्सुलेट पेपर का उपयोग करना आवश्यक है: विद्युत, संधारित्र, और इसी तरह। इसके अलावा, उपकरण को राल, वार्निश, एपॉक्सी यौगिकों और अन्य रासायनिक तत्वों के साथ लगाया जा सकता है जो सेवा जीवन का विस्तार करते हैं। खैर, उच्च दबाव पर वैक्यूम सिलेंडर के नीचे विभिन्न लीक को गर्म करने या हवा को बाहर निकालने की विधि का उपयोग करके आसानी से समाप्त कर दिया जाता है। हालाँकि, यदि मास्टर ने पहले प्रत्येक सूची से केवल एक तत्व का उपयोग किया है, तो नई तकनीक का उपयोग करके उत्पादन प्रक्रिया में विभिन्न कठिनाइयाँ उत्पन्न हो सकती हैं। इसके अलावा, लगभग निश्चित रूप से, ऐसी स्थिति एक तत्व के कारण होगी। हालांकि, यह गणना करना लगभग असंभव होगा कि कौन सा कारक डिवाइस के खराब प्रदर्शन को प्रभावित करता है। यही कारण है कि खराबी के कारण से शीघ्रता से निपटने के लिए बहु-कारक विश्लेषण पद्धति का उपयोग करने की अनुशंसा नहीं की जाती है, बल्कि एकल-कारक विधि का उपयोग किया जाता है।

बेशक, विभिन्न उपकरणों और उपकरणों का उपयोग करते समय जो किसी विशेष कारक के प्रभाव को ट्रैक करते हैंअंतिम परिणाम, अध्ययन को कई बार सरल बनाया जाता है, हालांकि, एक नौसिखिए इंजीनियर के लिए ऐसी इकाइयों का अधिग्रहण करना वहनीय नहीं होगा। यही कारण है कि विचरण के एकतरफा विश्लेषण का उपयोग करने की अनुशंसा की जाती है, जो आपको मिनटों में समस्याओं के कारण की पहचान करने की अनुमति देता है। ऐसा करने के लिए, यह आपके सामने सबसे संभावित परिकल्पनाओं में से एक को स्थापित करने के लिए पर्याप्त होगा, और फिर इसे प्रयोगों के माध्यम से साबित करना शुरू करें और डिवाइस के प्रदर्शन संकेतकों का विश्लेषण करें। बहुत जल्द, विज़ार्ड समस्याओं के कारण का पता लगाने में सक्षम होगा और किसी एक चयन को एक विकल्प के साथ बदलकर इसे ठीक कर पाएगा।
तीसरा उदाहरण
बहुभिन्नरूपी विश्लेषण का एक और उदाहरण। मान लीजिए कि एक ट्रॉलीबस डिपो दिन के दौरान कई मार्गों की सेवा कर सकता है। इन्हीं मार्गों पर, पूरी तरह से अलग-अलग ब्रांडों की ट्रॉलीबसें चलती हैं, और 50 अलग-अलग नियंत्रक किराया वसूलते हैं। हालांकि, डिपो का प्रबंधन इस बात में दिलचस्पी रखता है कि कुल राजस्व को प्रभावित करने वाले कई अलग-अलग संकेतकों की तुलना करना कैसे संभव है: ट्रॉलीबस का ब्रांड, मार्ग की दक्षता और कार्यकर्ता का कौशल। आर्थिक व्यवहार्यता को देखने के लिए, अंतिम परिणाम पर इन कारकों में से प्रत्येक के प्रभाव का विस्तार से विश्लेषण करना आवश्यक है। उदाहरण के लिए, कुछ पर्यवेक्षक अपना काम ठीक से नहीं कर रहे हैं, इसलिए अधिक जिम्मेदार कर्मचारियों को काम पर रखना होगा। अधिकांश यात्री पुरानी ट्रॉली बसों पर सवारी करना पसंद नहीं करते हैं, इसलिए नए ब्रांड का उपयोग करना सबसे अच्छा है। हालांकि, अगर ये दोनों कारक इस तथ्य के साथ जाते हैं कि अधिकांश मार्ग उच्च मांग में हैं, तो क्या यह किसी भी चीज के लायक है?परिवर्तन?

शोधकर्ता का कार्य अंतिम परिणाम पर प्रत्येक कारक के प्रभाव के बारे में यथासंभव उपयोगी जानकारी प्राप्त करने के लिए एक विश्लेषणात्मक विधि का उपयोग करना है। ऐसा करने के लिए, कम से कम 3 अलग-अलग परिकल्पनाओं को सामने रखना आवश्यक है, जिन्हें विभिन्न तरीकों से सिद्ध करना होगा। फैलाव विश्लेषण कम से कम संभव समय में ऐसी समस्याओं को हल करने और अधिकतम उपयोगी जानकारी प्राप्त करने की अनुमति देता है, खासकर अगर एक मल्टीफ़ेज़ विधि का उपयोग किया जाता है। हालांकि, ध्यान रखें कि एकतरफा विश्लेषण किसी दिए गए कारक के प्रभाव में बहुत अधिक विश्वास प्रदान करता है क्योंकि यह नमूने की अधिक विस्तार से जांच करता है। उदाहरण के लिए, यदि डिपो कंडक्टरों के काम का विश्लेषण करने के लिए अपने सभी प्रयासों को निर्देशित करता है, तो सभी मार्गों पर कई बेईमान श्रमिकों की पहचान करना संभव होगा।
एकतरफा विश्लेषण
एक-कारक विश्लेषण किसी विशेष मामले में अंतिम परिणाम के लिए एक निश्चित कारक का विश्लेषण करने के उद्देश्य से अनुसंधान विधियों का एक समूह है। इसके अलावा, दो कारकों के बीच सबसे बड़े प्रभाव की तुलना करने के लिए अक्सर एक समान तकनीक का उपयोग किया जाता है। यदि हम एक ही डिपो के साथ एक सादृश्य बनाते हैं, तो हमें पहले लाभप्रदता पर विभिन्न मार्गों और ट्रॉलीबस के ब्रांडों के प्रभाव का अलग-अलग विश्लेषण करना चाहिए, और फिर परिणामों की एक दूसरे के साथ तुलना करना चाहिए और यह निर्धारित करना चाहिए कि स्टेशन को विकसित करना किस दिशा में सबसे अच्छा होगा।

इसके अलावा, एक शून्य परिकल्पना के बारे में मत भूलना - यानी एक परिकल्पना जो नहीं करती हैखारिज किया जा सकता है और किसी भी मामले में यह एक डिग्री या किसी अन्य के लिए सूचीबद्ध सभी कारकों से प्रभावित होता है। भले ही हम केवल ट्रॉलीबस के मार्गों और ब्रांडों की तुलना करें, फिर भी कंडक्टरों के व्यावसायिकता के प्रभाव से बचा नहीं जा सकता है। इसलिए, भले ही इस कारक का विश्लेषण नहीं किया जा सकता है, शून्य परिकल्पना के प्रभाव को नहीं भूलना चाहिए। उदाहरण के लिए, यदि आप मार्ग पर लाभ की निर्भरता की जांच करने का निर्णय लेते हैं, तो उसी कंडक्टर को उड़ान पर जाने दें ताकि रीडिंग यथासंभव सटीक हो।
दोतरफा विश्लेषण

अक्सर, इस तकनीक को तुलना विधि भी कहा जाता है और इसका उपयोग दो कारकों की एक दूसरे पर निर्भरता की पहचान करने के लिए किया जाता है। व्यवहार में, आपको सटीक संकेतकों के साथ विभिन्न तालिकाओं का उपयोग करना होगा ताकि आप अपनी गणना और उन पर कारकों के प्रभाव में भ्रमित न हों। उदाहरण के लिए, आप एक ही समय में दो समान मार्गों पर दो पूरी तरह से अलग ट्रॉलीबस चला सकते हैं, शून्य परिकल्पना कारक की उपेक्षा करते हुए (दो जिम्मेदार कंडक्टर चुनें)। इस मामले में, दो स्थितियों की तुलना उच्चतम गुणवत्ता की होगी, क्योंकि प्रयोग एक ही समय में होता है।
दोहराए गए प्रयोगों के साथ बहुभिन्नरूपी विश्लेषण
इस पद्धति का प्रयोग व्यवहार में दूसरों की तुलना में अधिक बार किया जाता है, खासकर जब यह नौसिखिए शोधकर्ताओं के समूह की बात आती है। बार-बार अनुभव न केवल अंतिम परिणाम पर एक या किसी अन्य कारक के प्रभाव के बारे में आश्वस्त होने की अनुमति देता है, बल्कि अध्ययन के दौरान की गई गलतियों को भी खोजने की अनुमति देता है। उदाहरण के लिए, अधिकांश अनुभवहीन विश्लेषकएक या एक से अधिक अशक्त परिकल्पनाओं की उपस्थिति के बारे में भूल जाएं, जो अध्ययन के दौरान गलत परिणाम देती हैं। डिपो के उदाहरण को जारी रखते हुए, हम वर्ष के विभिन्न मौसमों में कुछ कारकों के प्रभाव का विश्लेषण कर सकते हैं, क्योंकि सर्दियों में यात्रियों की संख्या गर्मियों से बहुत अलग होती है। इसके अलावा, बार-बार अनुभव शोधकर्ता को नए विचारों और नई परिकल्पनाओं की ओर ले जा सकता है।
वीडियो और निष्कर्ष
हमें उम्मीद है कि हमारे लेख ने आपको यह समझने में मदद की है कि बहुभिन्नरूपी सहसंबंध विश्लेषण पद्धति किस पर आधारित है। यदि आप अभी भी इस विषय पर कोई प्रश्न पूछना चाहते हैं, तो हम अनुशंसा करते हैं कि आप एक छोटा वीडियो देखें। यह एक विशिष्ट उदाहरण का उपयोग करते हुए विचरण के विश्लेषण के तरीकों का विस्तार से वर्णन करता है।

जैसा कि आप देख सकते हैं, बहुभिन्नरूपी विश्लेषण एक जटिल, लेकिन बहुत ही रोचक प्रक्रिया है जो आपको अंतिम परिणाम पर कुछ कारकों की निर्भरता की पहचान करने की अनुमति देती है। इस तकनीक को जीवन के सभी क्षेत्रों में लागू किया जा सकता है और व्यवसाय करने के लिए प्रभावी ढंग से उपयोग किया जा सकता है। साथ ही, सरल तरीकों से सफलता के लक्ष्यों को प्राप्त करने के लिए बहुभिन्नरूपी विश्लेषण मॉडल का उपयोग किया जा सकता है।
सिफारिश की:
निर्णय मैट्रिक्स: प्रकार, संभावित जोखिम, विश्लेषण और परिणाम

हर पल चुनाव की समस्या, निर्णय लेने की कठिनाई का सामना करना पड़ा। अक्सर हम नहीं जानते कि सबसे अच्छा अभिनय कैसे किया जाए। सोचने में हमारा बहुत समय लगता है। शायद, हम में से प्रत्येक सीखना चाहता है कि कैसे जल्दी से सही, सबसे लाभदायक और सही समाधान खोजा जाए। दुनिया के सबसे अच्छे दिमागों ने एक अद्भुत निर्णय लेने की विधि विकसित की है - निर्णय मैट्रिक्स
स्थिति का विश्लेषण: विश्लेषण के विकल्प, विशेषताएं, चरण और परिणाम
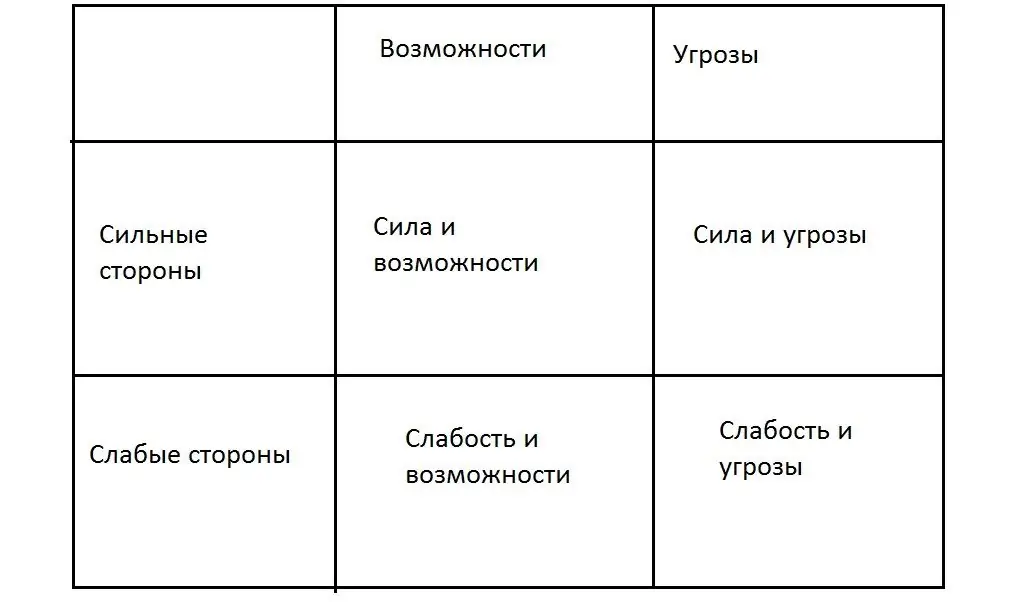
स्थिति विश्लेषण क्या है? कौन और कब इसे आयोजित करता है, स्थिति के विश्लेषण और मूल्यांकन के मुख्य चरण। स्थिति के विश्लेषण में प्रयुक्त तरीके और उपकरण। इसे क्यों किया जाना चाहिए? उद्यम के काम के लिए स्थिति के विश्लेषण का क्या महत्व है?
स्टॉक का विश्लेषण: संचालन के तरीके, विश्लेषण के तरीके चुनना, टिप्स और ट्रिक्स

स्टॉक क्या हैं। स्टॉक का विश्लेषण कैसे करें, इसके लिए सूचना के किन स्रोतों का उपयोग किया जाता है। शेयर खरीदने से जुड़े जोखिम क्या हैं? स्टॉक विश्लेषण के प्रकार, कौन से फॉर्मूले का उपयोग किया जाता है। रूसी कंपनियों के शेयरों के विश्लेषण की विशेषताएं क्या हैं, जानकारी एकत्र करने और शेयरों का विश्लेषण करने के लिए टिप्स और ट्रिक्स
कनेक्शन: उद्देश्य, कनेक्शन के प्रकार। यौगिकों के प्रकार के उदाहरण, फायदे, नुकसान

मशीनें और मशीन टूल्स, उपकरण और घरेलू उपकरण - इन सभी तंत्रों के डिजाइन में कई विवरण हैं। उनका उच्च-गुणवत्ता वाला कनेक्शन काम के दौरान विश्वसनीयता और सुरक्षा की गारंटी है। किस प्रकार के कनेक्शन हैं? आइए उनकी विशेषताओं, फायदे और नुकसान पर करीब से नज़र डालें।
संचार बिछाना: प्रकार, वर्गीकरण, बिछाने के तरीके और तरीके, संचार का उद्देश्य

बिछाने संचार निर्माण में सबसे महत्वपूर्ण चरणों में से एक है, उदाहरण के लिए, एक नए आवासीय भवन का। आज तक, संचार स्थापित करने के सबसे विविध तरीकों की एक बड़ी संख्या है। उनकी विशेषताओं, साथ ही फायदे और नुकसान ने इस तथ्य को जन्म दिया है कि प्रत्येक मामले के लिए एक व्यक्तिगत विधि का चयन किया जाता है।








